ロボットアームの位置制御
今回はロボットアームを直感的に動かす方法について、ご紹介します。
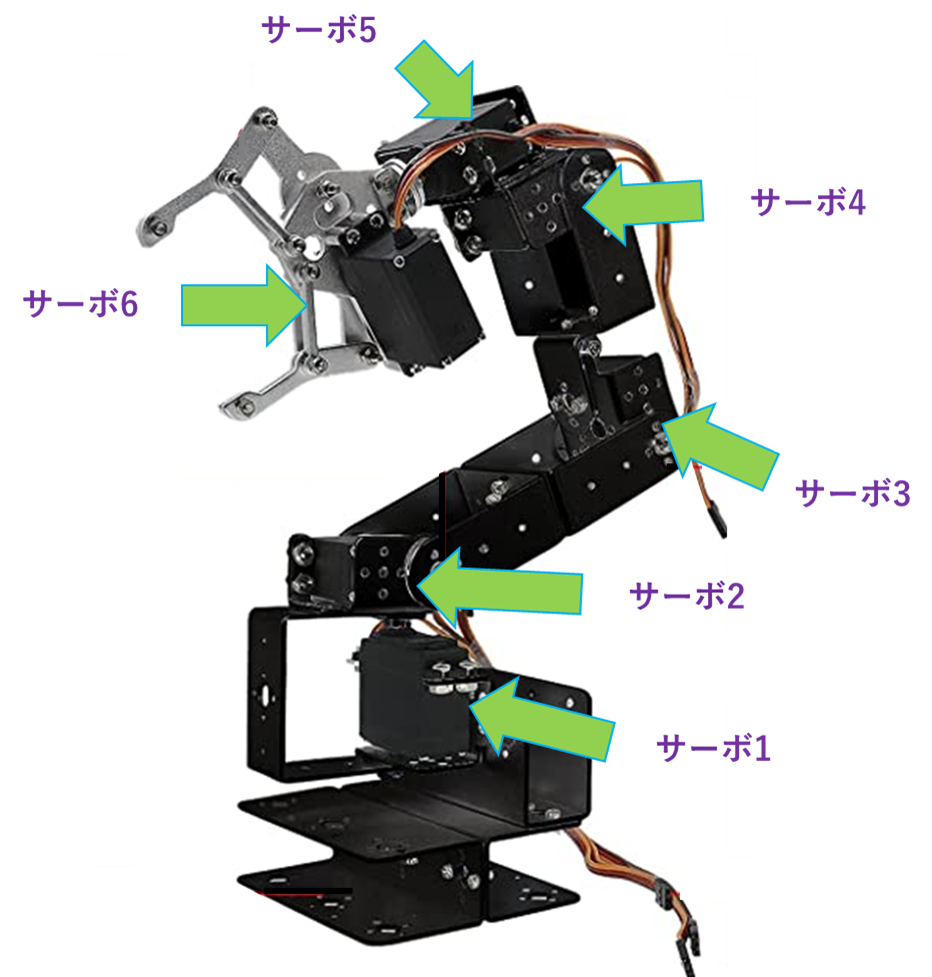
以下の記事でサーボモーターを組み合わせてロボットアームを作りました。
サーボモーターの回転角を指定するとロボットアームを動かせるわけですが、これだと直感的に操作できません。
指定した座標系にアームを動かしてくれる方が直感的に操作できるため、座標系を指定するとサーボモーターの回転角を逆算してくれるようにする方法をご紹介します。
この逆算するための学問が逆運動学です。
今回は、より簡単な座標系である円筒座標系でのロボットアームの位置制御を解説したいと思います。
円筒座標系の順運動学
以下は円筒座標系で、$θ_1$から$θ_3$は、サーボモーター1から3の角度です。
$L_2$はサーボモーター1から2までの長さ、$L_3$はサーボモーター2から3までの長さとし、ロボットアームの先端の位置を考えていきます。
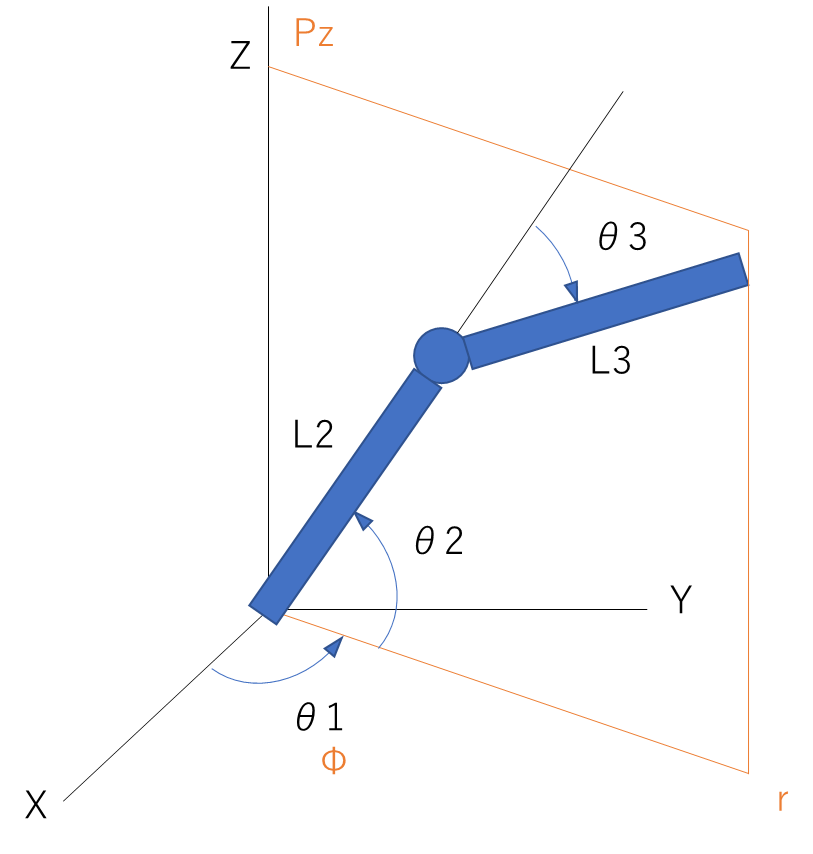
円筒座標系では、r-Φ-Pz軸を座標系としますが、$Φ$と$θ_1$は同じなので、r-Pz軸だけを求めればよく、比較的計算が楽です。
X-Y-Zを軸とする直交座標系は、円筒座標系の計算を発展させ、もう少し計算が大変になります。
まずは円筒座標系の計算から解説します。
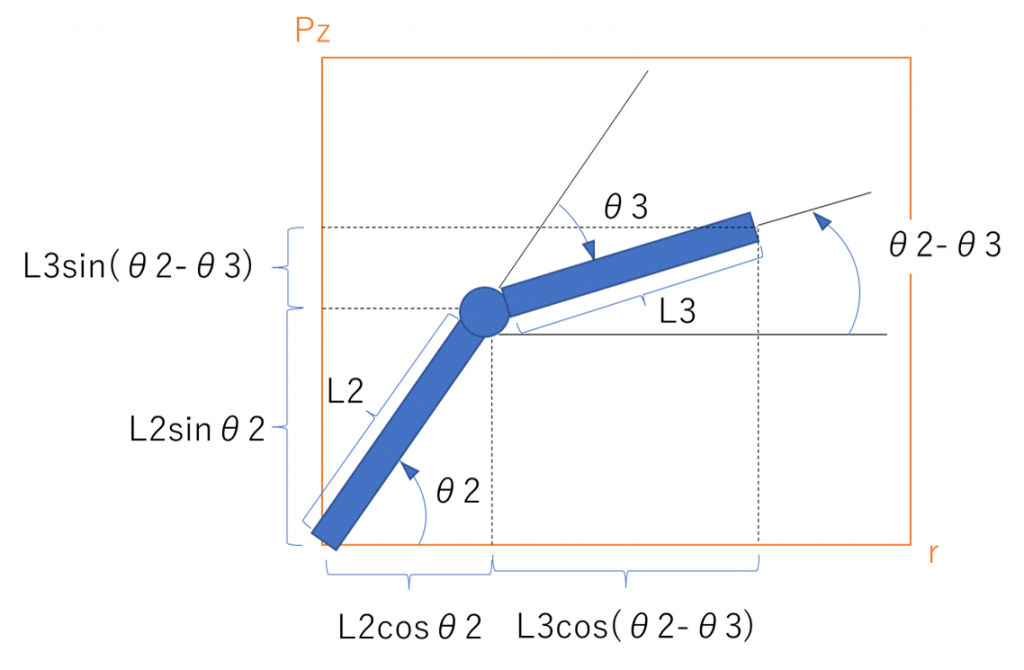
r-Pz軸だけ考えればいいので、上の図のようにし、サーボモーターの角度$θ_1$、$θ_2$、$θ_3$から円筒座標系の位置$r_{(t)}$、$Φ_{(t)}$、$Pz_{(t)}$を求めると
$r_{(t)}=L_2・C_2+L_3・C_{2-3}・・・(1)$
$Φ_{(t)}=θ_1・・・(2)$
$Pz_{(t)}=L_2・S_2+L_3・S_{2-3}・・・(3)$
ただし、
$C_{2}=Cos(θ_2)$
$S_{2}=Sin(θ_2)$
$C_{2-3}=Cos(θ_2-θ_3)$
となります。
円筒座標系の逆運動学
しかし、実際にロボットアームを制御する時は、座標系の位置を指定したいので、円筒座標系の位置$r_{(t)}$、$Φ_{(t)}$、$Pz_{(t)}$からサーボモーターの角度$θ_1$、$θ_2$、$θ_3$を求める必要があります。
そこで、(1)、(2)、(3)式から逆算して、$θ_1$、$θ_2$、$θ_3$を求めると
以下のようにサーボモーターの角度が計算できます。
$θ_1=Φ_{(t)}・・・(4)$
$θ_2=atan2[\dfrac{L_3S_3r_{(t)}+(L_2+L_3C_3)Pz_{(t)}}{(L_2+L_3C_3)r_{(t)}-L_3S_3Pz_{(t)}}]・・・(5)$
$θ_3=±Cos^{-1}[\dfrac{r_{(t)}^2+Pz_{(t)}^2-(L_2^2+L_3^2)}{2L_2L_3}]・・・(6)$
※ただし、$θ_3$は解が二つあり、プラスかマイナスのどちらか選ぶ必要あり
逆運動学の詳細計算
以下は詳細計算です。高校数学で解けるように計算手順を記載しました。
知らなくても上の式だけわかれば、制御はできますが、基礎計算を知っていれば、自由度を変えても応用が利くので、計算方法を載せています。
公式等忘れていてもわかるよう解説しているので、よければ読んでみてください。
$θ_1$の導出
(2)式より、そのまま$θ_1=Φ_{(t)}・・・(4)$
$θ_3$の導出
$θ_3$を求めるために$θ_2$を(1)、(3)式から除いていきます。
$r_{(t)}=L_2・C_2+L_3・C_{2-3}・・・(1)$
$Pz_{(t)}=L_2・S_2+L_3・S_{2-3}・・・(3)$
(1)、(3)式の両辺を二乗して加えます。
(1)式の二乗
$r_{(t)}^2=(L_2C_2+L_3C_{2-3})^2=L_2^2C_2^2+L_3^2C_{2-3}^2+2L_2L_3C_2C_{2-3}$
(3)式の二乗
$Pz_{(t)}^2=(L_2S_2+L_3S_{2-3})^2=L_2^2S_2^2+L_3^2S_{2-3}^2+2L_2L_3S_2S_{2-3}$

$Cos^2(X)+Sin^2(X)=1$
この公式を使うと
$L_2^2(C_2^2+S_2^2)=L_2^2$
$L_3^2(C_{2-3}^2+S_{2-3}^2)=L_3^2$ なので、
(1)式の二乗+(3)式の二乗の和は
$r_{(t)}^2+Pz_{(t)}^2=L_2^2+L_3^2+2L_2L_3(C_2C_{2-3}+S_2S_{2-3})$
となります。
$C_2C_{2-3}+S_2S_{2-3}$の部分は正式には
$Cos(θ_2)・Cos(θ_2-θ_3)+Sin(θ_2)・Sin(θ_2-θ_3)$なので、

$Cos(X-Y)=Cos(X)Cos(Y)+Sin(X)Sin(Y)$
この公式を使うと
$Cos(θ_2-(θ_2-θ_3))=Cos(θ_3)$となります。
よって、(1)式の二乗と(3)式の二乗の和は以下となり、$θ_3$だけの式になりました。
$r_{(t)}^2+Pz_{(t)}^2=L_2^2+L_3^2+2L_2L_3C_3$
逆三角関数を使って、$θ_3$は
$θ_3=±Cos^{-1}[\dfrac{r_{(t)}^2+Pz_{(t)}^2-(L_2^2+L_3^2)}{2L_2L_3}]・・・(6)$
となります。
ただし、$θ_3$はプラス・マイナス両方の解が出るので、制御時はどちらか選びます。
マイナスの解を選ぶとロボットアームがエビぞりになるので、今回はプラスの解を選択します。
$θ_2$の導出
長くなったので、再掲載します。
$r_{(t)}=L_2・C_2+L_3・C_{2-3}・・・(1)$
$Φ_{(t)}=θ_1・・・(2)$
$Pz_{(t)}=L_2・S_2+L_3・S_{2-3}・・・(3)$
$θ_2$を求めるために行列計算により、$S_2$、$C_2$を求めます。
(1)、(3)式を行列で表現すると
$\begin {bmatrix} r_{(t)} \\ Pz_{(t)} \end{bmatrix}=\begin {bmatrix} L_2・C_2+L_3・C_{2-3} \\ L_2・S_2+L_3・S_{2-3} \end {bmatrix}$
$Cos(X-Y)=Cos(X)Cos(Y)+Sin(X)Sin(Y)$ を使用すると
$C_{2-3}=C_2C_3+S_2S_3$
$Sin(X-Y)=Sin(X)Cos(Y)-Cos(X)Sin(Y)$ を使用すると
$S_{2-3}=S_2C_3-C_2S_3$
よって、
$\begin {bmatrix} r_{(t)} \\ Pz_{(t)} \end{bmatrix}=\begin {bmatrix} L_2・C_2+L_3・C_{2-3} \\ L_2・S_2+L_3・S_{2-3} \end {bmatrix}=\begin {bmatrix} L_2C_2+L_3C_2C_3+L_3S_2S_3 \\ L_2S_2+L_3S_2C_3-L_3C_2S_3 \end {bmatrix}$
$ \begin {bmatrix} a & b \\ c & d \\ \end {bmatrix} \begin {bmatrix} e \\ f \\ \end {bmatrix}=\begin {bmatrix} a・e+b・f \\ c・e+d・f \\ \end {bmatrix} $
$θ_2$を求めたいので、上の公式を使って、$C_2$、$S_2$の式に変形すると、
$\begin {bmatrix} r_{(t)} \\ Pz_{(t)} \end{bmatrix}=\begin {bmatrix} L_2C_2+L_3C_2C_3+L_3S_2S_3 \\ L_2S_2+L_3S_2C_3-L_3C_2S_3 \end {bmatrix}=\begin {bmatrix} (L_2+L_3C_3)・C_2+L_3S_3・S_2 \\ -L_3S_3・C_2+(L_2+L_3C_3)・S_2 \end {bmatrix}$
$=\begin {bmatrix} {L_2+L_3C_3} & {L_3S_3} \\ {-L_3S_3} & {L_2+L_3C_3} \\ \end {bmatrix} \begin {bmatrix} C_2 \\ S_2 \\ \end {bmatrix}$
$ A=\begin {bmatrix} a & b \\ c & d \\ \end {bmatrix} $
$ A^{-1}=\dfrac{1}{a・d-b・c}\begin {bmatrix} d & -b \\ -c & a \\ \end {bmatrix}$
上の公式を使って、$C_2$、$S_2$を求めると
$\begin {bmatrix} C_2 \\ S_2 \\ \end {bmatrix}={\begin {bmatrix} {L_2+L_3C_3} & {L_3S_3} \\ {-L_3S_3} & {L_2+L_3C_3} \\ \end {bmatrix}}^{-1}\begin {bmatrix} r_{(t)} \\ Pz_{(t)} \end{bmatrix} $
$\begin {bmatrix} C_2 \\ S_2 \\ \end {bmatrix}=\dfrac{1}{β}{\begin {bmatrix} {L_2+L_3C_3} & {-L_3S_3} \\ {L_3S_3} & {L_2+L_3C_3} \\ \end {bmatrix}}\begin {bmatrix} r_{(t)} \\ Pz_{(t)} \end{bmatrix} $
となります。$β=(L_2+L_3C_3)(L_2+L_3C_3)-L_3S_3・(-L_3S_3)$です。
βはこれ以降の計算にあまり関係ないので、そのままβと表記しておきます。
よって、$C_2$、$S_2$は
$\begin {bmatrix} C_2 \\ S_2 \\ \end {bmatrix}=\dfrac{1}{β} {\begin {bmatrix} {(L_2+L_3C_3)・r_{(t)}-L_3S_3・Pz_{(t)}} \\ {L_3S_3・r_{(t)}+(L_2+L_3C_3)・Pz_{(t)}} \\ \end {bmatrix}} $
$C_2=\dfrac{1}{β}{(L_2+L_3C_3)・r_{(t)}-L_3S_3・Pz_{(t)}}$
$S_2=\dfrac{1}{β}{L_3S_3・r_{(t)}+(L_2+L_3C_3)・Pz_{(t)}}$
$θ_3$の時とは異なり、$θ_2$に関しては、$C_2$、$S_2$がわかったので、解も一つに定まります。
$tan(θ_2)=\dfrac{S_2}{C_2}$より、
$θ_2=tan^{-1} [\dfrac{S_2}{C_2}]=tan^{-1} [\dfrac{L_3S_3・r_{(t)}+(L_2+L_3C_3)・Pz_{(t)}}{(L_2+L_3C_3)・r_{(t)}-L_3S_3・Pz_{(t)}}]$
ただし、実際の計算では、アークタンジェントの計算には$atan2(S_2, C_2)$を使用します。
細かい解説は省きますが、$atan2$は、引数が1つの時にアークタンジェントが解を1つに決められない問題を解決したアークタンジェントです。
違いは、値域が$- \dfrac{π}{2}$~$\dfrac{π}{2}$ではなく、$-π$~$π$となっており、より正確なアークタンジェントという認識で良いともいます。
プログラムに実装する時は、$atan2$を使用しないと誤動作の原因になるので、注意してください。
まとめ
以上が円筒座標系の逆運動学を利用したロボットアームの制御方法です。
上記を利用したプログラムは別途記事にするので、直感的に制御できることを確認していただけると幸いです!
また、より本格的な計算や制御の方法は以下の本がとても参考になるので、興味のある方はぜひ読んでみてください。
参考書籍
このシリーズの他の記事
この記事は、おまけ②です。



コメント